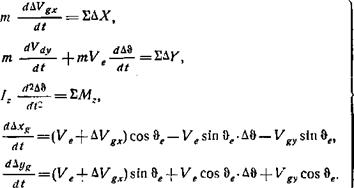В неспокойной атмосфере

§ 2.1. ПОСТАНОВКА ЗАДАЧИ

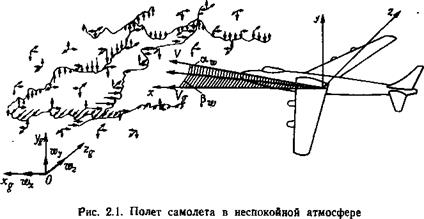
На рис. 2.1 схематически изображен полет самолета в неспо­койной атмосфере. В каждой точке пространства вектор скоро­сти ветра W может быть представлен в виде суммы проекций [10] на оси земной системы координат xg, yg, zg._На рис. 2.1 показаны лишь проекции переменной составляющей w вектора ветра.

Самолетные оси х, у, z являются связанными осями. Как по­казано на рис. 2.1, при порывах ветра скорость самолета относи­тельно воздуха {воздушная скорость) V отличается от путевой скорости Vg как по величине, так и по направлению (углы aw и рш). Изменение величины и направления вектора скорости V приводит к появлению дополнительных сил и моментов, дейст-

вующих на самолет и вызывающих возмущение исходного режи­ма полета.

При очень сильных порывах ветра возмущения исходного ре жима полета могут стать весьма значительными, и самолет може — выйти на срывные режимы (с нарушением как устойчивости, таї и управляемости полета). Исследование таких режимов полет;: необходимо проводить по полным системам уравнений движенш самолета без линеаризации и разделения движения на продоль ное и боковое. Подобные задачи чрезвычайно сложны, не подда­ются аналитическому исследованию в общем виде и в данной книге не рассматриваются.

Большинство же других задач динамики полета в неспокойной атмосфере вполне удовлетворительно описывается линеаризован­ными уравнениями, раздельно для продольного и бокового дви­жения самолета. Такая методика позволяет получить общие решения для исследуемых случаев полета, причем результаты тео­ретического анализа достаточно хорошо согласуются с результа­тами летного эксперимента вплоть до срывных режимов.

В заключение этого параграфа сделаем несколько замечаний относительно системы самолетных осей. Ось х системы связанных самолетных осей х, у, г, используемых в этой книге, направлена не по хорде крыла, как обычно, а по направлению путевой ско­рости в невозмущенном режиме Ve. Скорость Ve составляет с хор­дой крыла угол <хе — невозмущенное значение угла атаки в ис­ходном режиме. Поэтому при составлении уравнений моменты инерции следует пересчитать к новым осям. Если известны момен­ты инерции относительно главных осей инерции самолета /[11]г, Л/г. /я — и угол А в плоскости симметрии самолета между направлени­ем главных и связанных осей, то значения моментов инерции в связанных осях определяются формулами:

/Х = /ХГС08*Д + /,Г8ІП*Д, /y = /*rsin2 Д-f /yrCOS2 Д, | А»=Лг. Лгу = у (Л: г-/у г) Sin 2Д, Гуг = /2Х = 0. (2П

Взаимное положение земных (хе, yg, zg) и самолетных связан­ных осей (х, у, z) показано на рис. 2.2. Связанные оси изображены в произвольном положении, которое они занимают вместе с са­молетом в какой-либо момент возмущенного движения. Переход связанных осей в это произвольное угловое положение из исход­ного* (хь у и 2i), соответствующего невозмущенному режиму, производится с помощью трех поворотов, которые должны выпол­няться в следующем порядке:

1) поворот на угол рыскания ф вокруг зертикальной оси у. в результате которого оси занимают положение *2, Уг, *2, а ось х занимает окончательное положение по курсу;

2) поворот на угол тангажа Ф вокруг горизонтальной оси г2, в результате которого оси занимают положение Хз, уз, гз, а ось х занимает окончательное положение по тангажу;

3)

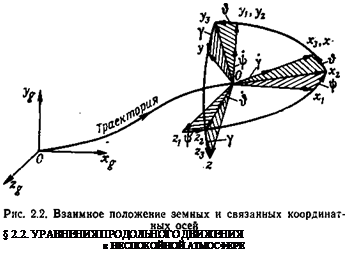поворот на угол крена у вокруг оси х (или Хз, так как они совпадают), в результате которого все оси занимают окончатель­ное положение х, у, г.

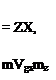Чтобы получить возможно более простые уравнения динамики самолета, не будем учитывать целый ряд явлений, оказывающих относительно малое влияние на движение самолета. Пренебрежем связью между продольным и боковым движениями и будем счи­тать самолет жестким телом [12] постоянной массы. При указанных допущениях уравнения динамики продольного движения в свя­занных осях имеют вид [26, 27]:

В уравнениях (2.2);

m — масса самолета;

Vgx, Vgy — проекции путевой скорости самолета на связан-

wgi — проекция угловой скорости самолета относитель­но земли на связанную ось г;

1г — момент инерции самолета относительно связан­ной оси г;

%Х, ЕК — суммы проекций внешних сил на оси х и у;

ЕЛТг — сумма проекций моментов внешних сил относи­тельно ОСИ Z.

Внешние силы складываются из аэродинамических сил, силы веса самолета и силы тяги. Для этих сил и создаваемого ими мо­мента относительно оси z используем следующие соотношения: Е* = — Gsind —*(а, V, М, р)-j-Рх(8Д) М, р, Т)= ’

—— G sin & — CfS + Рх>

ЕГ= — Geos &+К(а, V, М, р) + Ру (8Д, М, р, Г) = = _Gcos» + C^-^- + Py,

В уравнениях (2.3):

О — вес самолета; а — угол атаки;

8Д — угол поворота органа управления авиадвига­телем;

8„ — угол отклонения руля высоты;

V — скорость самолета относительно воздуха;

M — Via, где а — скорость звука на высоте полета;
р— плотность воздуха;

Рх, Ру—проекции силы тяги двигателей на оси х и у; S — площадь крыльев; р — давление воздуха;

Т— абсолютная температура воздуха;

Сх— коэффициент лобового сопротивления;

Су—коэффициент подъемной силы; тг—коэффициент аэродинамического момента от­носительно оси 2;

Ьа — средняя аэродинамическая хорда.

Уравнения (2.2) дополним следующими кинематическими со­отношениями:

=У*г’с08в-К, у5ІП

= Vgx sin & 4- Vgy cos

где xg, yg — координаты центра тяжести самолета в земных осях.

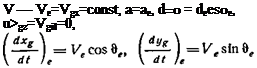Выберем в качестве невозмущенного режима прямолинейный равномерный полет в вертикальной плоскости при отсутствии ветра. В этом невозмущенном режиме параметры движения само­лета имеют следующие значения (индексом «е» будем отмечать невозмущенный режим):

Вводя небольшие отклонения всех параметров от их значений в невозмущенном режиме и отбрасывая члены с произведением отклонений параметров, на основании (2.2) и (2.4) получим урав­нения движения в отклонениях:

(2.5)

В уравнениях (2.5) отклонения параметров от их исходного значения в невозмущенном режиме обозначены значком Л. У па­раметров, которые в невозмущенном режиме равны нулю (щи Увв), значок Д здесь и ниже опускается.

Особенность уравнения динамики (первые три уравнения сис­темы 2.5) при анализе движения в неспокойном воздухе заклю­чается в том, что в соответствии с (2.3) в правые части этих урав­нений входят параметры, характеризующие движение самолета относительно воздуха (воздушная скорость V, угол атаки а и т. п.). Левые же части этих уравнений, учитывающие инерцион­ные силы и момент, которые определяются движением относи­тельно земли, имеют такой же вид, как при движении самолета в неподвижном воздухе. Эти силы и момент определяются состав­ляющими путевой скорости и второй производной угла тангажа.

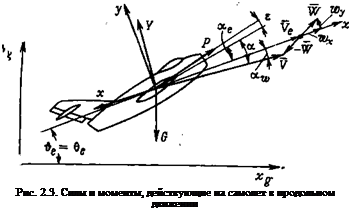
Для удобства анализа сил и момента введем некоторые допол­нительные кинематические соотношения, которые учитывают дви­жение воздуха. Эти соотношения приближенно справедливы в предположении малости скорости ветра по сравнению со ско­ростью самолета:

Wy,

___ і „ I _ _________ _ Vgy . wy

л==ле~-ag-raw=ae———————- 7}—— Г ~r~ ■

v e » e

В (2.6):

wx, [13]°y — составляющие вектора ветра по осям земной сис­темы координат, у которой ось xg совпадает с на­правлением связанной оси х в невозмущенном ре­жиме;

— приращение угла атаки за счет изменения на­правления вектора путевой скорости

—

приращение угла атаки за счет составляющей ветра w„.

Первые два соотношения в (2.6) вытекают из очевидного век­торного равенства _ _ _

V = Vg-W. (2.7)

Соотношения (2.6) поясняются рис. 2.3*. Кроме параметров движения, уже обозначенных выше, на рис. 2.3 показан угол е между направлением хорды крыла и вектором тяги Р.

Перейдем к анализу правых частей уравнений динамики само­лета в неспокойном воздухе (первые три из уравнений (2.5)].

Разлагая функции, входящие в (2.3), в ряд Тейлора по их аргументам и сохраняя только член ряда с первой степенью при­ращения аргумента, получим следующие выражения для прира­щений сил и моментов:

ЪХ=— G cos ЬеАЬ — Xvg[14]AVgx — Xw*wx — Хмт — — XveyVgy-xw, ywy — Xy±yg—PMCOS (a, 4 s)am +

-f pp cos (ae 4 e) P*byg+PTcos (a, 4 e) Tvbyg+

4- Я* cos (ae — f є) Д8д,

EK=G sin + Yve*bVgx+Yw*wx+Г^ДМ+

4 К vwV& 4 К"ле>,++PM sin (ae+є)ДуИ +

+ />/» s in (а,+є) рУАуе 4- p T sin (ae 4- e) Ту A yg4
4Р*8Іп(«,4е)Д8д,

Шг=МьгА 4 ми* Wgx+ M?*WX+M? AM 4 M? gyVgy 4
4 Mfywy 4 Mvzgy J^SL 4 Ml У JlL. 4 Міру Ayg.

Запись различных величин с индексом вверху есть сокращен­ное изображение частной производной от этой величины по пара­метру, определяемому данным индексом. Например, Xv*x— =dX/dVgx и т. д.

Производные по Vgy и wy отражают зависимость сил и мо­ментов от угла атаки, определяемую соотношением (2.6). Произ­водные по путевой скорости (по Vgx и Vgy) должны в принципе отличаться от производных по скорости ветра (по wx и wy), так как изменение путевой скорости происходит сравнительно мед­ленно, тогда как порывы ветра на летящий самолет действуют с большой частотой. Это обстоятельство будет учтено ниже ме­тодами нестационарной аэродинамики. Здесь же будем полагать, что производные по соответствующим параметрам одинаковы как для путевой скорости, так и для скорости ветра.

Необходимо особо остановиться на моменте, который создает­ся в результате запаздывания скоса потока от крыла на опере­нии. Учет этого явления для сравнительно медленных изменений угла атаки крыла сводится к введению в третье выражение (2.8) члена с dVygjdt (соответствующего а). Так как угол атаки а в со­ответствии с (2.6) зависит от скорости вертикальных порывов, то формально в этом выражении появляется член с dwv/dt, учиты­вающий запаздывание в образовании на оперении скоса потока от ветра. Однако по отношению к порывам самолет здесь и по­чти * везде ниже рассматривается как точка, вследствие чего не учитывается запаздывание в образовании подъемной силы на горизонтальном оперении, создаваемой вертикальными порыва-
ми, по сравнению с образованием ее на крыле. В § 3.5 показано, что даже для больших самолетов такое упрощение вполне допу­стимо. Тем более допустимо не учитывать запаздывание скоса потока на оперении, обусловленного порывами ветра. По указан­ным обстоятельствам ниже член с производной от ветра (dwjdt) в уравнении моментов относительно оси z учитываться не будет.

а*Д»-‘ dAVgx

Подставляя в (2.5) значения приращений сил и моментов из (2.8) и производя несложные преобразования, получаем систему уравнений, описывающих продольное движение самолета в не­спокойной атмосфере:

„ Гск ■-c’xb‘yex — CZ ——— Oi Vgy — dfi 1 * dt x g* У dt y gy

= «еД8д + axWx + ay’Wy^

dt d*yg dt

={Ve—ДVgx)sinft* — f Ve cos V дд + V y cos 0,.

— — СгАЪ в + Cx Wx — C-y Wy,

Формулы для расчета коэффициентов уравнений (2.9) приве­дены в табл. 2.1.

В табл. 2.1 приняты следующие обозначения:

_ g — ускорение силы тяжести;

гг=У /Jmlbt — безразмерный радиус инерции самолета отно­сительно оси г;

|*п—т1?еЬ£’— относительная плотность самолета (в продоль­ном движении); *

‘2£=tnlpeSVe—единица относительного времени;

_ =Ьйтг1Уе — безразмерная угловая скорость;

а=-^г——безразмерная скорость изменения угла атаки.

Система уравнений (2.9) составлена для общего случая него­ризонтального полета и является достаточно громоздкой. Первое упрощение, которое можно сделать без существенного снижения общности результатов анализа, состоит в выборе горизонтального полета в качестве невозмущенного режима. В этом случае

Коэф­ фици­ ент	•	Формула	Размер­ ность
ч	g cos ье	МСЄКГ2
а- X	_J_ Гс, 1 СММ P*COS(*e+t) ] ,, Iе" + 2 с* М — SuV*.
а. У	~2^(Суе~ ^	сек-1
ау	ve %хе? е	2Pp cos (a* + є) py 2P T cos (ae + e) ТУ СхерУ———————————————- SV2 SV2	сек—2
Ч	Ph cos (ае + t)jm	M СЄК—2
h	g sinftg	M СЄК““2
ь. X	1 к,+іс>,+ рЛ,‘7’+"| ^ L 2 у SfeVgUg J	сек-1
Ь. У	*, w+c")	СЄК—1
h	V, ^хе? е	2Pp sin (ae + s)рУ 2P T sin (ae + e) ТУ 1 CyeVy + + 2 1 SV* SV2e J	сек—2
Ьь	РГі sin (ае — f z)/m	JK С^ЛГ—2
ь*	-с*./2t#	сек—1
%	-»п"*/2т,7*	сек—1
с. X	— m^„Me/2xl7l	М^сек—1
С- У	— m IWeiJr	сек—1
с. У	— nfy.„l2Vetf? l	М^сек—1
сь		сек—2
сз		сек—2

At*

ax Wgx — f a-y Vgy=a-xwx+aywy, + b-yV*y=-b-xW*Jrb-yWy’ +c-W„r-C"

___ 2L-C-V = At >’* ** у dt У *y = — C^bt—C-xWx-C-y’Wy,

= sin 9y, = fr» =0 И COS Ъе = 1. Кроме того, в первом и втором урав­нениях системы (2.9) можно отбросить члены, учитывающие из­менение высоты, так как эти члены оказываются существенно меньше остальных. Поскольку современные системы управления не воздействуют на авиадвигатель, не будем учитывать члены с 6Д. В результате уравнения (2.9) приобретают вид

Эта система уравнений описывает как короткопериодические, так и длиннопериодические движения самолета.

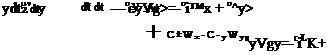Как будет показано в гл. 3, для решения большинства практи­чески интересных задач динамики полета в турбулентной атмо­сфере система уравнений (2.10) может быть существенно упро­щена. Это упрощение заключается в пренебрежении изменением скорости вдоль оси х при полете в турбулентной атмосфере (AVrg*=0). В результате первое и четвертое уравнения из систе­мы (2.10) выпадают. Случаи, когда такое допущение приводит к принципиальным ошибкам, будут ниже оговорены особо. Пре­небрегая ДVgx, из (2.10) получаем:

= VM+V„.

Эти уравнения применяются для описания короткопериодиче­ского движения самолета.

Иногда бывает удобнее выразить все функции, входящие в (2.11), в форме угловых величин. Используя для этих целей (2.6), получаем (без учета продольной составляющей ветра):

da„

(д *>-«*)• dt e e

Коэффициенты (2.12) связаны с коэффициентами (2.11) следую­щими зависимостями: ba= — b-y, = — VeCy, ca=—Vec^.

Уравнения (2.11) и (2.12) достаточно точно описывают коротко­периодическое движение самолета и будут в дальнейшем широко использоваться.

Уравнения (2.9) — (2.12) позволяют исследовать динамику са­молета с зажатым или двигающимся по некоторому закону рулем высоты в неспокойном воздухе. Однако в настоящее время само­леты в течение значительной части из общего времени полета уп­равляются автопилотом. Поэтому представляет интерес рассмот­рение динамики самолета с автопилотом.

Для анализа динамики полета с автопилотом уравнения про­дольного движения самолета должны быть дополнены уравнени­ем (законом управления) автопилота. При математическом опи­сании автопилота будем пользоваться уравнениями идеального автопилота, т. е. будем пренебрегать временем запаздывания и нелинейностью его характеристик. Допустимость такого подхода в рассматриваемой задаче будет специально обоснована в § 3.3.

В настоящее время используются два типа автопилотов: с жесткой обратной связью и со скоростной обратной связью. Наибольшее распространение получили автопилоты первого ти­па. Примером автопилота с жесткой обратной связью может слу­жить автопилот АП-6Е.

Закон управления этого автопилота для канала руля высоты имеет вид

4= -*>(д»3-щ+ь *2L-ИА’*, (2.13)

где г»— передатЬчное отношение (число) для угла тангажа Ф, величина безразмерная;

— передаточное отношение (число) для угловой скоро­сти oz, размерность — сек-,

iy— передаточное отношение для высоты yg, размерность — рад/М или град/М;

Д1>з— заданное приращение угла тангажа.

В режиме стабилизации горизонтального полета ДФ3=0. Иногда целесообразно исключить из закона уравнения член, про­

порциональный высоте. В этом случае для режима стабилизации угла тангажа в горизонтальном полете получим

(2.14)

Закон управления автопилота со скоростной обратной связью для канала руля высоты можно записать в следующем виде [28]:

л. і — 1, (2.15)

dt 9 J * dt ‘ ь d& y

где iq — передаточное отношение для угла тангажа, размер­ность — сект1;

/* — передаточное отношение по <о2, безразмерное;

— передаточное отношение по ю2, размерность — сек.

В результате объединения уравнений самолета (2.10) и авто­пилота (2.13) получаем систему уравнений, описывающих про­дольное движение самолета с автопилотом в неспокойной атмо­сфере:

rdSV,

dt

——b-&V ~-b-V = — b-w ~b-w

e dt ux v gx I dt І у v gy UXUUX I Uу wy>

Г Ctiycb C} Wx-CpWy,

VeM+Vgy.

biv*y=-biwx+b}Vy>

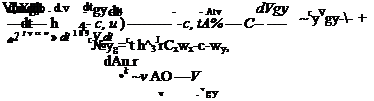Если объединить с уравнением автопилота упрощенные урав­нения самолета (2.11), то получим: